ECUACIONES VECTORIALES
DEFINICIÓN
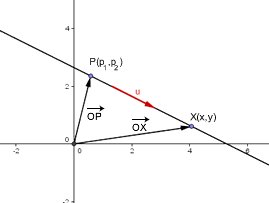
Para determinar la ecuación vectorial de una recta es necesario que conozcamos un punto de la recta y un vector de posición o dos puntos de la recta. Vamos a hallar la ecuación a partir de un punto y un vector de posición, si tubiesemos dos puntos A, B entonces el vector AB es un vector de posición.
La ecuación de una recta es una expresión analítica que permite identificar todos los puntos de la recta.
Dados un punto 
de la recta y un vector de dirección 
, un punto genérico de la recta 
tendrá como vector de posición 
.
Es claro que 
, como el vector 
y están en la misma dirección existe un número 
tal que 
, por tanto 
esta expresión se conoce como ecuación vectorial de la recta.
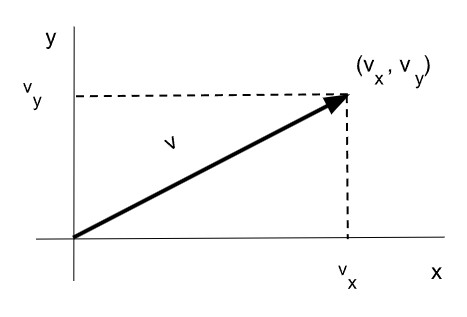
Módulo de un vector
El módulo de un vector representa su longitud. Debido que se trata de la hipotenusa de un triángulo rectángulo, se calcula mediante el teorema de Pitágoras como la raíz cuadrada de la suma de sus componentes elevadas al cuadrado.
En física, se llama módulo de un vector a la norma matemática del vector de un espacio euclídeo ya sea este el plano euclídeo o el espacio tridimensional. El módulo de un vector es un número que coincide con la "longitud" del vector en la representación gráfica.
El concepto de norma de un vector generaliza el concepto de módulo de un vector del espacio euclídeo.
En R2 se calcula como:
Tangente de un ángulo
Tangente de un ángulo
La tangente es en trigonometría una herramienta relacionada con el seno y el coseno, razones que ya hemos estudiado. Ahora veremos más de cerca que es la tangente de un ángulo. Como ya sabemos los triángulos rectángulos son básicos en el estudio de la trigonometría. La tangente de un ángulo es la razón entre la longitud del cateto opuesto del ángulo dividido entonces por el largo del lado adyacente del ángulo.
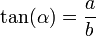
Ejercicios
Ejercicios
c)
c)
Tan°=3/4
Tan°=3/4
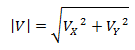
Los vectores se los encuentra en nuestra vida cotidiana,existe en una figura podremos encontrar lo que es bidimensional (A,B)y la tridimensioonal que incluye (X,Y,Z), existe una cuarta diemension que es irreal.Tambien se puede decir que un vector es un elemento de un espacio vectorial del que, en ocasiones, especialmente en física y geometría, interesa conocer su longitud.
ResponderBorraren esta clase lo que yo entendí es que los ecuaciones vectores nos permiten encontrar explicaciones de manera concreta sobre objetos, fenómenos o sucesos que se dan en nuestro entorno dándonos a conocer las direcciones de objetos como: sus dimensiones que posees tanto las podemos ver como las que no se puede ver en la que nos puede ayudar a determinar su angulo. este sistema se puede emplear en cualquier momento de nuestra vida como para saber la explicación de algún objeto que se este visualizando.
ResponderBorrarPor lo que pude entender de la clase denominamos un vector a un segmento de recta, contado a partir de un punto del espacio, cuya longitud representa a escala una magnitud, en una dirección determinada y en uno de sus sentidos, es un proceso sencillo de asimilar y fácil al momento de calcular su tangente en las figuras de diferentes dimensiones,la real de 2 dimensiones y las irreales de 3,4 o más dimensiones
ResponderBorrarEn esta clase vimos la aplicacion de un vector por ende el vector tiene tres características esenciales: módulo, dirección y sentido. Para que dos vectores sean considerados iguales, deben tener igual módulo, igual dirección e igual sentido.
ResponderBorrarLos vectores se representan goemétricamente con flechas y se le asigna por lo general una letra que en su parte superior lleva una pequeña flecha de izquierda a derecha
Los vectores son magnitudes plasmadas en un espacio tridimensional "x, y, zona" O bimensional"b, y" Que son las más utilizadas para la resolución de las mismas estos vectores constan de una tangente y un vector que debemos encontrar |v|.
ResponderBorrarEsta clase es muy interesante pues se trata de vectores que son direcciones u orientaciones que en su gráfico es una flecha que se dirige a un cierto lado, por lo cual lo que busca su expreción es la dirección exacta y magnitud, además se requiere sacar el angulo cuando los objetos estan en dos dimenciones.
ResponderBorrarNombre: Leidy Iralda Lavanda Sanchez
ResponderBorrarLo que puedo opinar acerca del tema explicado ecuaciones vectoriales permiten determinar cada punto ( X-Y) de cualquier recta.Todo esto se aplica en la vida cotidiana.
Nombre:Lupe Xiomara Apariencia Veliz
ResponderBorrarEn esta clase vimos lo que es vectores.
Un vector es el que dirige a una recta dados los puntos podemos fácilmente obtener el vector que hay entre ellos. Encontrando el ángulo y facilmente encontramos la tangente que lo encontramos en la gráfica.
Los vectores son magnitudes que se encuentran en la vida cotidiana ademas en el plano tridimensional en donde las coordenadas son X,Y,Z
ResponderBorrarLas ecuaciones vectoriales las encontramos en todo momento de nuestra vida por la bidimensional (x,y,z) con las ecuaciones vectoriales podremos resolver ecuaciones de tres incognitas ya que los resultados que salgan en x,y,z mediante el reemplazo de valores podremos saber si esta bien realizado el proceso y tambien es un largo proceso.
ResponderBorrarLos vectores varían según el significado del contexto quedando definido por un módulo dirección u orientacion.
ResponderBorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarMaría Cristina Sánchez Rivas
ResponderBorrarEn esta clase mi aportación es sobre el tema ecuaciones vectoriales pude determinar una ecuación vectorial obteniendo el ejercicio se pude aplicar su
correspondiente y así encontramos el ángulo
Gracias
Este tema sobre las ecuaciones vectoriales es muy importante ya que podemos resolver un ejercicio teniendo un vector de posición o dos puntos de la recta y se puede hacer operaciones (suma y resta).
ResponderBorrarNombre: Claudia Yeleni Maldonado Herrera
ResponderBorrarLas ecuaciones vectoriales son cuando pasan por el punto A y es paralela al vector, para realizar una recta en el plano son necesarios dos puntos aqui encontramos el vector que es el que dirige cualquier dirección de la recta y luego podemos encontrar la tangente
La ecuación de una recta es una expresión analítica que permite identificar todos los puntos de la recta. El módulo de un vector representa su longitud. Debido que se trata de la hipotenusa de un triángulo rectángulo, se calcula mediante el teorema de Pitágoras como la raíz cuadrada de la suma de sus componentes elevadas al cuadrado.La tangente es en trigonometría una herramienta relacionada con el seno y el coseno, razones que ya hemos estudiado.
ResponderBorrarSegún lo que investigue sobre el tema pude averiguar que dentro de las propiedades que tienen el modulo de un vector están la relación con el producto escalar en la cual la suma de los vectores esta relacionado con el producto escalar y la desigualdad triangular en la que la suma de dos vectores es menor o igual que la suma de módulos.
ResponderBorrarLos vectores son de mucha importancia que con un punto o dos en él plano cartesiano podemos obtener él origen, direccion, modulo y sentido encontrando magnitudes escalares y vectoriales que con operaciones matemáticas podemos llegar a su solución.
ResponderBorrarLos vectores se basan en la vida diaria y en el plano tridimencional (x,y,z) y se lo puede resolver utilizando despeje de ecuaciones
ResponderBorrarSon muy importantes por que en un plano cartesiano podemos encontrar una dirección o magnitudes.
ResponderBorrarlas tridimensional x,y,z y
Los vectores se los puede considerar como lo que acontece en l vida cotidiana por que todo lo que nos rode esta en tres dimenciones osea que las cosas son tridimencionales y que varian segun la perspectiva de lo qe se quiere obtener es decir los vecotores varian en sus dimenciones como lo son x,y,z .
ResponderBorrarBásicamente la ecuación de la recta es una expresión analítica que permite identificar todos los puntos de la recta, así mismo para determinar la ecuación vectorial de una recta es necesario que conozcamos un punto de la recta y un vector de posición o dos puntos de la recta.
ResponderBorrarNombre:Joselyn Madelaine Oyola Loja
ResponderBorrarBien se ha definido vectorial de una variable real en el espacio, en forma similar se puede definir funcion vectorial de un variable real en el plano y tambien en el espacio n-dimensional.
Los vectores se basan en la vida diaria y son de mucha importancia esta la podemos resolver por medio de tres incognitas tambien se cabe decir que un vector es un elemento de un espacio vectorial
ResponderBorrarNombre: Ricardo Bryan Capa Caamaño
ResponderBorrarEsta clase me pareció muy interesante ya que vimos como la ecuación 1 se conoce con el nombre de ecuación vectorial y nos sirve para que en una recta conozcamos un punto de la recta y el vector de posición o dos puntos de esta recta.
Muy buena explicación tomando en consideración que sólo pueden haber suma y restas dependiendo de los elementos que tengamos en el vectorial.
ResponderBorrarAsí mismo podemos ver cuál es la tangente que va a tener el resultante del vector.
Por eso es bueno saber como irá el valor para incluirlo en el resultante considerando también el signo de la operación.