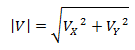ECUACIONES VECTORIALES
DEFINICIÓN
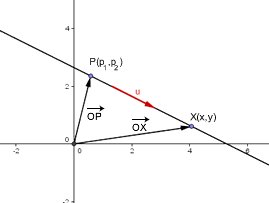
Para determinar la ecuación vectorial de una recta es necesario que conozcamos un punto de la recta y un vector de posición o dos puntos de la recta. Vamos a hallar la ecuación a partir de un punto y un vector de posición, si tubiesemos dos puntos A, B entonces el vector AB es un vector de posición.
La ecuación de una recta es una expresión analítica que permite identificar todos los puntos de la recta.
Dados un punto  de la recta y un vector de dirección
de la recta y un vector de dirección  , un punto genérico de la recta
, un punto genérico de la recta  tendrá como vector de posición
tendrá como vector de posición  .
.
Es claro que  , como el vector
, como el vector  y
y  están en la misma dirección existe un número
están en la misma dirección existe un número  tal que
tal que  , por tanto
, por tanto  esta expresión se conoce como ecuación vectorial de la recta.
esta expresión se conoce como ecuación vectorial de la recta.
Módulo de un vector
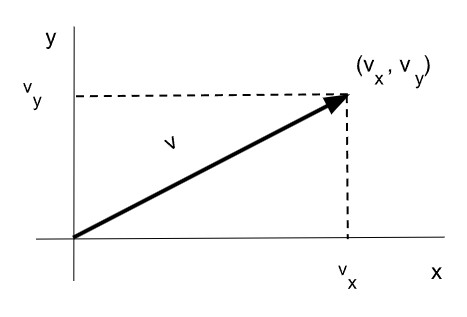
El módulo de un vector representa su longitud. Debido que se trata de la hipotenusa de un triángulo rectángulo, se calcula mediante el teorema de Pitágoras como la raíz cuadrada de la suma de sus componentes elevadas al cuadrado.
En física, se llama módulo de un vector a la norma matemática del vector de un espacio euclídeo ya sea este el plano euclídeo o el espacio tridimensional. El módulo de un vector es un número que coincide con la "longitud" del vector en la representación gráfica.
El concepto de norma de un vector generaliza el concepto de módulo de un vector del espacio euclídeo.
En R2 se calcula como:
Tangente de un ángulo
Tangente de un ángulo
La tangente es en trigonometría una herramienta relacionada con el seno y el coseno, razones que ya hemos estudiado. Ahora veremos más de cerca que es la tangente de un ángulo. Como ya sabemos los triángulos rectángulos son básicos en el estudio de la trigonometría. La tangente de un ángulo es la razón entre la longitud del cateto opuesto del ángulo dividido entonces por el largo del lado adyacente del ángulo.
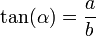
Ejercicios
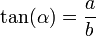
Ejercicios
Tan°=3/4
Tan°=3/4